“毕达哥拉斯证明方法失传后，欧几里得给了证明方法。”闻琪生看着他逐渐专注的神，“这是一能衍生代数问题的几何问题，比如说，345这样的正整数组，满足a︿2＋b︿2=c︿2，他有多少组？”

小胖顺着他手指的地方看着那个图形，不知是不是他的错觉，在那修长的手指、以及萌萌胖胖的小辟邪的映衬下，小三角不再显得令人讨厌，而是——有那么一丝可了！

小胖：“……”

“……我作业的时候，也、也能那样写……吗？”

这个现在在他前的人，于他而言，确实是非常特别的人。

然而……

“……是、吧？”

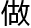
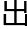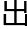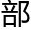“后来欧拉了n=3，n=4时的证明，更多就力所不及了。直到95年，也就是300多年后的英国数学家怀尔斯给了全证明。”

“是，比如3、4、5；5、12、13；7、24、25等……证明方式……设a=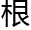号2b＋1，b，c=b＋1，三数互质。”闻琪生怕他觉得无趣，又延伸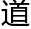：“当时为了证明，有个还算有趣的故事。有这么一个老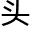儿，他的墓志铭是这样写的：过路的人！这儿埋葬着丢番图。请计算下列数目，便可知他一生经过了多少寒暑。他一生的六分之一是幸福的童年，十二分之一是无忧无虑的少年。再过去七分之一的年程，他建立了幸福的家。五年后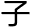儿生，不料儿竟先其父四年而终，只活到父亲岁数的一半。晚年丧老人真可怜，悲痛之中度过了风烛残年。请你算一算，丢番图活到多大，才和死神见面？”

“我们说回它。”闻琪生指了指胖嘟嘟的辟邪隔的直角三角形：“其实，勾数的缘起也很早，公元前2600年前，古埃及人就已经发现了345是一组勾数。但那时候，没有成为定理。”

角形旁边画了一只胖嘟嘟的神兽，有像狮，张着大嘴小尖牙，脑袋上着个独角，趴坐着，“在中国它正式现是在西汉时期，之后宋朝末年蒙古侵、明朝末年清军关……等到了清朝，辟邪已经完全狮化……江时代正式随东渡的汉人日本，借着影视行业发扬。”

“有……很多、无限组？”小胖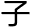语气不那么确定。

闻琪生看他：“怎么了？”

他又开始说辟邪的起源，提及苏尔王朝，提及殷周、秋战国时期。

小胖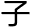很认真的问。

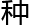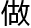“恩，这数叫勾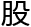数，也叫毕达哥拉斯三元数组。”他在三角形旁边写下公式（3n）︿2＋（4n）︿2=（5n）︿2，“那么当abc互质的情况下，他还是无穷多组吗？”

小胖：“……”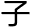

“……”钱多伸手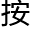住他，“再、再说一遍。”

闻琪生看到小胖星星看着自己，莫名其妙的生一丝自得——他从来不是喜卖学识的人，也不屑于用它们去换取别人的曲意奉承。

“你好厉害！！！”在钱多看来，闻琪生能据自己一个走神说来的词而给他延伸了这么多的知识，神话、宗教、文化……一切信手拈来、侃侃而谈，简直像是世界上没有他不知的东西。

“这个很简单，待会儿把题目写下来你就知了。”闻琪生说，“丢番图是代数之父，他写的中，就证明了勾数有无穷多组。后来，有一个法国的律师，名叫费，看了后，就在书角写：‘当整数n　＞2时，关于x，　y，　z的方程　x︿n　＋　y︿n　=　z︿n　没有正整数解。地方太小，证明过程我就不写了。’——这就是费大定理。”