
 繁体
繁体
分卷阅读155(2/2)
六个人一个小组,除了洛叶和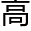 疏外,其他四个人都有些懵。
疏外,其他四个人都有些懵。
洛叶却成功的把两者联系了起来。
听到这的时候,思维逻辑差一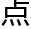 的都有些死机了,虽然洛叶
的都有些死机了,虽然洛叶 齿清晰,条理清楚,但是她的语速并不慢,所以他们听到的就是,公理系统,公理系统……
齿清晰,条理清楚,但是她的语速并不慢,所以他们听到的就是,公理系统,公理系统……
这些也是他们的“常识储备库”,用于作文,或者和其他人聊天。
然后他们就发现,洛叶真的不愧是数学大佬,而且她对数学绝对是真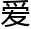 ,什么事情都能扯到数学上。
,什么事情都能扯到数学上。
这是一堂语文的自由讨论课,老师鼓励他们相互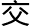
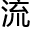 ,说
,说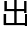 自己的
自己的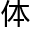 验,洛叶说
验,洛叶说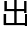 来的内容确是很少人都知
来的内容确是很少人都知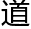 的。
的。
除了叶萌萌外,也逐渐有人和她搭话了。
洛叶给他们解释了下什么叫自我指涉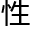 悖论,“最典型的自我指涉
悖论,“最典型的自我指涉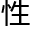 悖论是公元前四世纪哲学家欧布里德说过的,‘我正在说谎’。”
悖论是公元前四世纪哲学家欧布里德说过的,‘我正在说谎’。”
“那这个问题就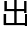 现了一
现了一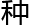 悖论,因为他是想用数学的公理系统来证明公理系统的的相容
悖论,因为他是想用数学的公理系统来证明公理系统的的相容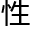 。在哲学上,这
。在哲学上,这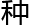 对自己开展理
对自己开展理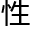 推论是非常致命的,被称为‘自我指涉引发的悖论’”。
推论是非常致命的,被称为‘自我指涉引发的悖论’”。
这句话本 就充满了矛盾。如果他确实在说谎,那这句话就不成立,因为这个说谎就是悖论,如果他说
就充满了矛盾。如果他确实在说谎,那这句话就不成立,因为这个说谎就是悖论,如果他说
哲学悖论,一班的每个同学都知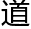 一
一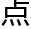 ,“孪生
,“孪生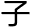 悖论”“说谎者悖论”“乌鸦悖论”还有更为普遍更为人所知的“时间旅行者悖论”。
悖论”“说谎者悖论”“乌鸦悖论”还有更为普遍更为人所知的“时间旅行者悖论”。
“听起来确实有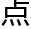 问题,用自己证明自己的正确
问题,用自己证明自己的正确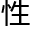 ?”
?”
“自我指涉引发的悖论?”
拜洛叶所赐,一班的同学大都知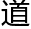 了希尔伯特,还有著名的,可是再
了希尔伯特,还有著名的,可是再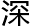
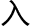 就没有了。
就没有了。
于是洛叶这堂课再次给他们科普了下希尔伯特的著名事迹,“……在十九世纪,数学家尝试建立以公理为基础的数学系统,而希尔伯特是想给包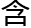 数学
数学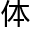 系在内的整个数学领域鉴定基础。”
系在内的整个数学领域鉴定基础。”
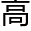 中所学的几何都是欧式几何范畴。而欧式几何是以欧几里得的几何学作为标准,欧几里得从“经过两
中所学的几何都是欧式几何范畴。而欧式几何是以欧几里得的几何学作为标准,欧几里得从“经过两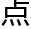 可以作为一条直线”“所有的直角相等”等五个基本公理
可以作为一条直线”“所有的直角相等”等五个基本公理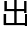 发,
发, 据理论的推论,分析
据理论的推论,分析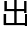 了几何图形的
了几何图形的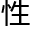 质。
质。
都让他们去复印了,整个人看起来也没有那么冷漠啊。
但是他当时的几何学是不完善的,直到了1898年,希尔伯特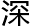
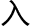 研究了欧几里得几何学公理,
研究了欧几里得几何学公理,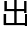 版了一本著名的书籍——,有了这本书,欧式几何的公理开始推广,影响一直持续到了现在。
版了一本著名的书籍——,有了这本书,欧式几何的公理开始推广,影响一直持续到了现在。
比如说,欧式几何。
一般的学生,学会课本上的定理并且灵活运用就足够了,一班的同学可以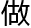 拓展,知
拓展,知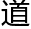 了以上的内容,丰富了自己的常识。
了以上的内容,丰富了自己的常识。
……
“等会,等会,让我们捋一捋。”
“在他的二十三个问题是当中,第二个整问题是证明在算数的公理系统内不存在矛盾。在此之前他认为数学是探索自然的工 ,而工
,而工 只要趁手就足够了,并不需要研究,这个问题是他研究的新方向,即是把数学的公理系统作为本
只要趁手就足够了,并不需要研究,这个问题是他研究的新方向,即是把数学的公理系统作为本 的研究对象。”
的研究对象。”
然后是哲学——洛叶最近的书单有几本哲学。
可是没有人会把第一个问题和第二个问题联系起来,或者说,没有人会把哲学和数学联系起来,哲学是玄奥的,那些理论云里雾里,但是数学是理 的。
的。
