而在那篇论文中他并没有给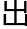完整的解题方法，可以想象那个时候他应该也没有完全解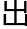来，而来这里的目的就不言而喻了。

足以可见他为什么被称之为几何皇帝的接班人了。

而舒尔茨去年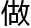这个报告的时候还是博士生，他的报告给这个猜想的破译提供了一个新的方向。

作者有话要说：　　午安

洛叶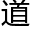,“这并不妨碍我研究代数几何。”

而Weight-monodromy猜想是在数论相关的奖项里仅次于哥德赫猜想,黎曼猜想这样的著名猜想，同时这是德利涅教授的研究成果之一。

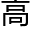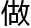舒尔茨的研究范畴主要是代数几何，数论，对群论也只能说是有所研究，他没有因为这个难度很就认为洛叶不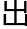来的，因为他本就是那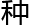让人瞠目结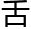的天才，他能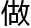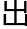来，别人自然也能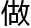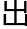来。

而看懂他这篇报告，需要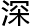厚的代数几何功底,不然光是理解霍奇理论就能让崩溃。

这是去年舒尔茨受邀在数学会上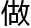报告提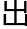的概念，刚刚提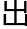来就引发了一场革命,为一些正式无法解决的问题提供了新的曙光。

而洛叶此时已经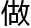到了舒尔茨边，“我看过你的论文，完状空间。”

洛叶说的完状空间是代数几何和算术几何的概念。

舒尔茨闻言再次诧异的看了洛叶，二十四维的圆球堆集，绝对是一个非常复杂的数学结构，而且在群论和李代数范畴，这是一个非常重要的数学结构，如果她真的能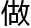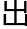来，她绝对可以获得学士学位，甚至是一篇四大数学论文预定了。

洛叶，“我最近研究圆球堆集，如果研究了结果，我应该会因此获得学士学位，我之后也应该再转战代数几何领域。”

“二十四维。”

☆、189

代数几何研究的基本对象是一个称为代数簇的象空间。从浅显的方向来理解,一个簇是一些多项方程的解集,再无法理解,可以尝试想象一下，把多项式的系数看作实数空间，所得的簇是一个易于看到的几何空间，一个三维椎的表面。

这两个概念相连起来，关系到一个主题——上同调理论。或者说这个研究关乎到千禧难题排名第二的霍奇猜想。

学神真的仰望就足够了，近距离绝对会让人窒息的。

“就像是这并不妨碍你研究Weight-monodromy猜想。”

他没有询问下去，而是继续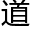，“关于霍奇

接下来的2章都会有大量的数学理论，不喜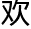看的不要买了。

舒尔茨既然最近在国，还跑来上课，自然听过洛叶的名字了，“我以为你研究的是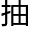象代数。”

了一起，和他们在一个课堂上，让他们呼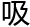都不由的沉重了起来。

对于这位最新崛起的数学家，洛叶自然平时也多有关注，甚至把他的博士论文研究了一遍，在那篇论文中，他不仅开创了一个PS理论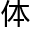系，还在最后提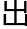了对Weight-monodromy猜想的试探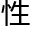的解析方法。

而完状空间大的，它像是分形几何，但是却又不是分形，只表现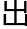了分形的一些特征,锯齿状的结构和分形的整无限层次,他们也类似于一个数学螺旋,一个永不封闭的无限嵌螺旋。

“多少维？”