布德，“那应该很快了。”

其他人纷纷摇了摇，“我看报，最近欧洲数学会要在这里召开，他们应该是来参加的人吧。”

洛叶当然不会和他说真的原因，只是，“等我硕博的时候应该会选择代数几何。”

这个时间正值暑假，来欧洲旅行的不少，比较年轻的像是学生一样的人就忍不住的看向他们两人，有一个还忍不住拍了照片，悄悄的询问同桌，“你们能听得懂他们在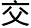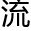什么吗？”

他比洛叶这个学生要忙多了，在不得不结束和她的谈话时，非常诧异的问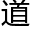，“你对几何学的认识明显比代数学要好，为什么要选择的群论？”

欧洲数学会的影响力差不多仅次于世界数学会，在这样的会上，

本群。”

“他们看起来一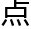不像是数学家啊。”

布德也没有想到他居然可以和洛叶基本上没有障碍的下去，不但是曲率和基本群，洛叶懂黎曼几何，辛几何，拓扑几何，分形几何，有些涉猎他自己都没有她来的广。

在他们印象中，数学家应该都是发白，年过半百，可无论是布德还是洛叶都颠覆了他们的想象，这也太年轻了。

欧洲数学会主要是面向于在欧洲工作以及欧洲籍贯的数学家，布德拿到博士学位后就开始在斯坦福担任教授，现在在哥比亚大学任教，可以说他已经许久没有回过欧洲了，这次回来，不但要准备报告，还要和一众故人联络。

等布德走后，洛叶收好了纸条，吃完剩下的东西才继续上楼。

他20岁就拿到了博士学位，和他比洛叶的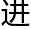度算是慢了，可是经过刚刚的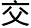谈，他相信只要他愿意，应该会很快拿到硕士学位和博士学位，他匆匆写下了自己的邮箱，“如果你在微分几何上有什么问题可以和我讨论。”

他们是外行，可是餐厅却不乏有内行，他们是绝对认得布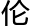德的，看着他居然和一个小女生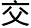谈甚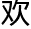，他们都不由的想一睛，确定没有错之后，看洛叶的神就多了几分奇异。

而在旁人看来，两人完全是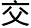谈甚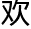，而在他们旁边的人完全听不懂他们两个在讨论什么。

等到布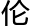德的报告讲完，下面响起了烈的掌声，趁着这掌声洛叶悄然离去。

“尤其是那个女生，看起来好小。”

而光是一个补充，是无法支撑过一个小时的报告会的，在讲完这个泛函方程后，他又开始讲起了让自己之前发表过微分球面定理（DifferentialSphereTheorem），也是对那篇论文一个重要补充，讲其中一个关键，三维行几何。

第二天布德的报告会，洛叶也去听了，下面的满满的，其中不乏知名的数学家。

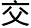“……任何致，可定向的三维行，当用其中一些整正互补相互的球面和环面去切，对一个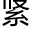致单联通的黎曼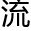行，它的截面曲率位于……”

“……在截面曲率拼挤条件下，常曲率空间形式中的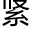致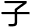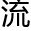行拓扑同胚于球面，当大于四维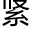，致定向的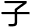行满足于……”

而布德的补充主要是在对于在他证明武义-劳森猜想中运用的的一个泛函方程，正是因为这个泛函方程，让他有了灵光一闪，最终用一个简单无比的方式来证明了这个猜想。