维，从理论上来讲，每上升一个维度计算的难度和工程量都会上升，而洛叶却要反其而行,想用简单的方式来证明,就像是布德证明的武义-劳森猜想，在八维的尝试证明中，洛叶不甚满意，等扩展到了她现在行二十四维，更不满意了。

代数几何方面的著名数学家法尔廷斯给布德颁发了这个奖项，舒尔茨也受邀席了这次的欧洲数学会，只是他的是45分钟的报告，他的风比布德劲，可比不得布德这几年发表的论文，和积累的成果。

洛叶站在他边，跟随着众人一起鼓掌，“下一次的EMS（欧洲数学会奖简写）应该属于你了。”

而莫扎尼卡研究这个问题，发明了一个公式，可以回答这个问题，她以这个公式发表了三篇论文，分别刊登在四大期刊的三家期刊上——。

洛叶在下面听的十分专注，时不时的笔记，不得不说，这只存在于象空间的几何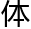对洛叶来说更为有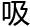引力，而且在莫扎尼卡说自己如何想到那个充满了创意的方程，一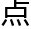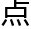的让它变成现在的完整模样，怎么在脑海构建这么一个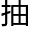象几何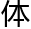，给了洛叶十分大的启发。

“拉

它自从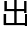现就成了几何学的中心之一，被无数狂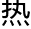的数学家研究，可是它的存在就是不可思议的，所以它也是不可攀的，研究到了现在，一些简单的问题都没有解决掉。

可以说等这次欧洲数学会结束的时候，洛叶还意犹未尽，这样平的报告会哪里有那么容易见到？再次见到恐怕要等14年的世界数学会了，而下次的欧洲数学会要等16年。

比如在双曲面上的“直线”——在数学上被称为测地线，也就是最短路径问题。因为双曲面上，有些测地线可以无限延长，像是普通二维平面上的直线一样，有些却是封闭的曲线，所以数学家无法清楚在双曲面上到底有几条测地线。

是最近几年最为引人注目的数学家之一。

两人这段时间都在保持着不太频繁的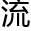，洛叶知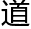他最近的研究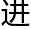度，他现在撰写的论文准备投递给。

洛叶决定多去听一听报告。

洛叶第二天听的报告是一位女数学家，玛杨·莫扎尼卡，在数学界中女数学家很少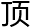，尖的女数学家更少，而莫扎尼卡就是其中一位堪称尖的数学家，最为擅长的领域是黎曼曲面，模空间，几何学。

她的报告是关于双曲面的。

既然从象代数的角度找不到更优的路径，那不如引其他理论。

双曲面状似甜甜圈，拥有两个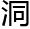以上的曲面，它可以说在三维空间无法存在，只存在于数学家想象中的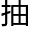象空间，曲面的距离和角度只能以一组特殊的方程来测量，如果双曲面上存在虚拟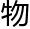生，那生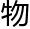在双曲面上的任意一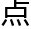都像是鞍。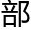

她回去之后找了许多曲面的相关的论文，熬了一夜后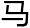不停蹄的接着奔赴报告会场。

而这次的欧洲数学会会奖落在了布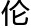德上。

就差一个拿到大满贯。

而她无法找到一条更为简单的路径，在接连听了布德和威腾的报告后,让她有了新的想法。

而她的报告正是对这个公式的详细的补充和说明，下面坐满了人。

舒尔茨，“还要四年……”