当然，亚历山大本是很服气这个奖项最终给了洛叶，尤其是在看到了洛叶才引爆了整个数学界的论文后，更认为这个奖项名至

洛叶饶有兴趣的看着书架上的书籍名字，怎么说呢，普林斯顿的人文学术气息特别厚，他们的图书馆收藏的书籍，期刊等也全都属于那严肃类型的，而斯坦福大学的图书馆似乎要活泼一，在数学区居然还有趣味数学这样的书收藏。

斯坦福大学的图书馆容量不比普林斯顿来的差，而且也有他们学校独有的孤本，除了和唐纳森讨论ACC猜想，洛叶就喜来他们图书馆借阅材料。

他的准备特别充分，证明自己有和洛叶合作的实力。

洛叶抬看去，一个材大的年轻男生手里捧着一堆书，穿着简单的T恤和仔，看起来和图书馆内的其他人并没有什么分别，“洛，我是亚历山大。”

希尔伯特把费大定理比喻为会下的金母。

他没能写下这个猜想的证明结果，后来欧拉在写给哥德赫的信中证明了N=3，后来尔曼，狄利克雷，加布里尔在那个猜想写下后的两百年后证明了五次幂和七次幂。

“还是真的是因为写不下而放弃了？”

能在这个区域碰到，而且能一认来洛叶的，恐怕也只有数学专业的了。其实如果洛叶有看数学相关的一些报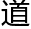，应该能认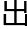来亚历山大，去年和她一起竞争Mon奖的最大对手，如果没有洛叶，亚历山大已经拿下了这个奖项。

这个猜想本就是一个很有名的数学故事。

直到1954年，谷山-志村猜想建立了椭圆曲线和模形式之间的联系，这是费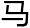大定理破解的重要一步，证明了这个猜想就可以证明费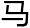大定理成立，可是最终费大定理被彻底证明是在1995年，中间又经过了无数的无数的波折。

看完这本书后大概就能认识到数学界大分的名人，中间还有哥德尔，伽罗瓦，图灵等人当初试图证明这个定理的分思路，洛叶看的津津有味，尤其是那些最终证明失败的思路，让洛叶觉得十分有借鉴意义。

“斯坦福研究生。”

在费写下这个著名的猜想时，“一个立方数是不能够表示成两个立方数之和的，四次方也同理，将一个于2次幂的数分解为两个同次幂的数之和都是不可能的。可写成当整数n>2时，关于x，y，z的方程x^ny^n=z^n没有正整数解.。”

ACC这样的猜想并不是一朝一夕可以完成的，洛叶也不可能一直待在斯坦福，他们只能在洛叶在这里的几天内，讨论阶段的成果。

费大定理是业余数学家之王埃尔·德·费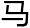在三百多年写的一个著名数学猜想。

写完这段话后，他的这张纸要用完了，就又写到，“我有一个对这个命题十分妙的证明，这里空白太小，写不下。”

费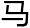本是解析几何的发明者之一，概率论的主要创始人，在微积分上，他的贡献仅次于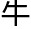顿和莱布尼茨。

忽然有人轻声，“你觉得费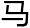当时是真的想到了证明方式了吗？”

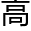“斯的代数基本定理，斯图默的个数问题，阿贝尔不可能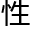定理，卡斯迪朗问题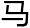，尔法问题……”

现在她手边就有一本在。